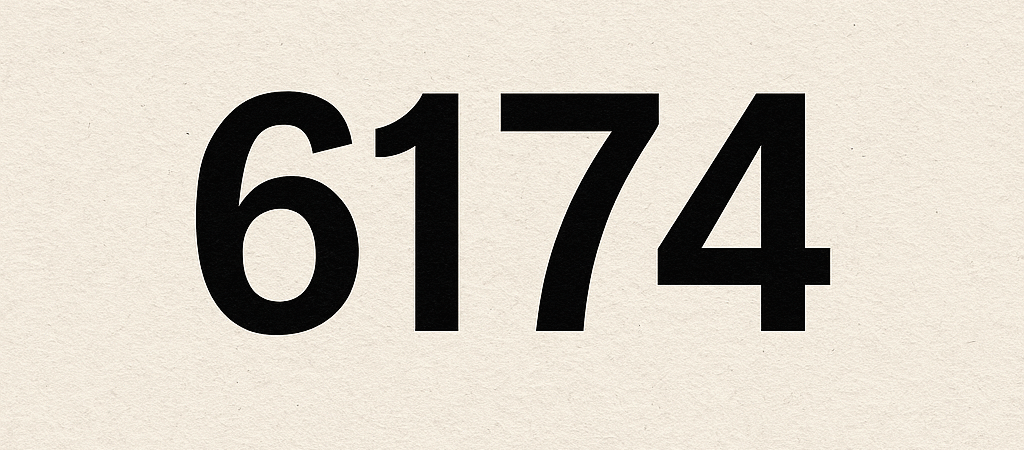Numbers have always carried an aura of mystery and fascination that attracts mathematicians and the curious alike.
Some may seem simple and dull at first glance, but they hide surprising properties that defy intuition.
One of the most intriguing examples is the number 6174, known as Kaprekar’s Constant, a mathematical phenomenon that shows how certain numerical patterns can appear almost “magically.”
🧠 The Man Behind the Mystery: D. R. Kaprekar
Dattatreya Ramchandra Kaprekar, a self-taught Indian mathematician born in 1905, was the discoverer of this curious constant.
Kaprekar devoted much of his life to studying the properties of numbers, working mostly independently and developing concepts that still surprise the mathematical community today.
Among his most notable contributions are Kaprekar’s Constant, the Kaprekar process, and Kaprekar numbers—all tied to numerical patterns that seem to emerge from nowhere.
What’s most fascinating about Kaprekar isn’t just the math, but his way of finding beauty in what appears to be simple: a four-digit number.
To him, every number could be a small work of art—if only we knew how to look at it.
✨ The Magic of 6174
The S&P500 lingered at 6174 for only a few minutes: the market showed little sensitivity to the mysteries of mathematics.
At first glance, 6174 looks like a normal four-digit number.
In reality, it’s much more: it’s Kaprekar’s Constant.
By following a specific procedure with any four-digit number that has at least two different digits, you will always and inevitably arrive at 6174—in no more than seven steps.
Here’s the process:
- Take any four-digit number with at least two different digits.
- Arrange its digits in descending order to form the “larger” number.
- Arrange the digits in ascending order to form the “smaller” number.
- Subtract the smaller number from the larger one.
- Repeat the process with the result until you reach 6174.
Surprisingly, regardless of the starting number, after a few iterations you’ll always reach 6174—and from that point on, the process will always return 6174.
For example, let’s choose the number 3524:
- Step 1: Descending order → 5432
- Step 2: Ascending order → 2345
- Step 3: Subtract → 5432 – 2345 = 3087
Now repeat with 3087: - Step 1: Descending → 8730
- Step 2: Ascending → 0378
- Step 3: Subtract → 8730 – 0378 = 8352
Again, with 8352: - Step 1: Descending → 8532
- Step 2: Ascending → 2358
- Step 3: Subtract → 8532 – 2358 = 6174
There you have it! In just three steps, we arrive at the mysterious constant, which will repeat eternally with the same process.
🔍 Why 6174 Is So Fascinating
What makes 6174 truly incredible isn’t just how it works, but the inevitability of the result.
No matter the starting number—except for a few exceptions like numbers with all identical digits (e.g., 1111, 2222, 9999, where the constant doesn’t apply)—the process always converges to this constant.
This gives 6174 an almost mystical quality: it acts like a “magnet” in the world of four-digit numbers.
From a mathematical perspective, Kaprekar’s Constant illustrates how order and structure can emerge from apparent chaos.
From a sequence that may seem random or arbitrary, a solid and predictable pattern emerges.
This property has not only fascinated mathematicians but has also become a classic example in recreational mathematics, showing how even simple numbers can hide deep secrets.
🎓 Educational and Recreational Applications
Kaprekar didn’t just discover this constant—he showed how numbers can be an intellectual playground.
Math teachers use 6174 to teach concepts such as:
- Number sorting
- Patterns and convergence
- Properties of subtraction and numbers
It’s also a great example to introduce students to logical thinking and iterative process analysis.
Games and math challenges have even been created based on this process, where participants try to reach Kaprekar’s Constant from any number in the fewest steps possible.
🔢 A Parallel with Other Numerical Phenomena
Kaprekar wasn’t the only mathematician to discover surprising patterns in numbers.
For example, the number 1729, known as the Hardy-Ramanujan number, has the property of being the smallest positive integer that can be expressed as the sum of two cubes in two different ways:
1729 = 1³ + 12³ = 9³ + 10³
It’s obviously hard to prove that it’s the smallest such number—but trust me, the proof is a bit complex.
Both examples—6174 and 1729—show how certain numbers possess special properties that set them apart in the vast numerical universe.
Though they may appear ordinary at first glance, these numbers reveal the existence of hidden patterns that can only be discovered through analysis and mathematical curiosity.
🌟 A Reflection on the Beauty of Mathematics
The number 6174 reminds us that mathematics is not just a tool for solving practical problems—it’s also a source of beauty and wonder.
Kaprekar found magic in the routine of numbers, showing that even a common number like 3524 can be transformed into something extraordinary through a creative and logical process.
Such discoveries also teach us something important about patience and observation: truth is often hidden in plain sight, and only by exploring repeated patterns and processes can we reveal the underlying harmony in what seems chaotic.
Though Kaprekar’s Constant may seem to belong solely to the world of recreational mathematics, there are valuable lessons that traders can learn.
One of the clearest is the importance of patterns and repetition.
Just as any number converges to 6174 after repeating a process, financial markets can also reveal patterns over time if studied carefully.
Patience, discipline, and careful observation are essential to identifying these patterns and making informed decisions.
Moreover, Kaprekar’s story reminds us that seemingly chaotic things can have hidden structure.
📈 Mathematics for Trading
When you discover something in finance that works like Kaprekar’s Constant, you’ve uncovered a hidden algorithm of the market—that’s how trading systems are born.